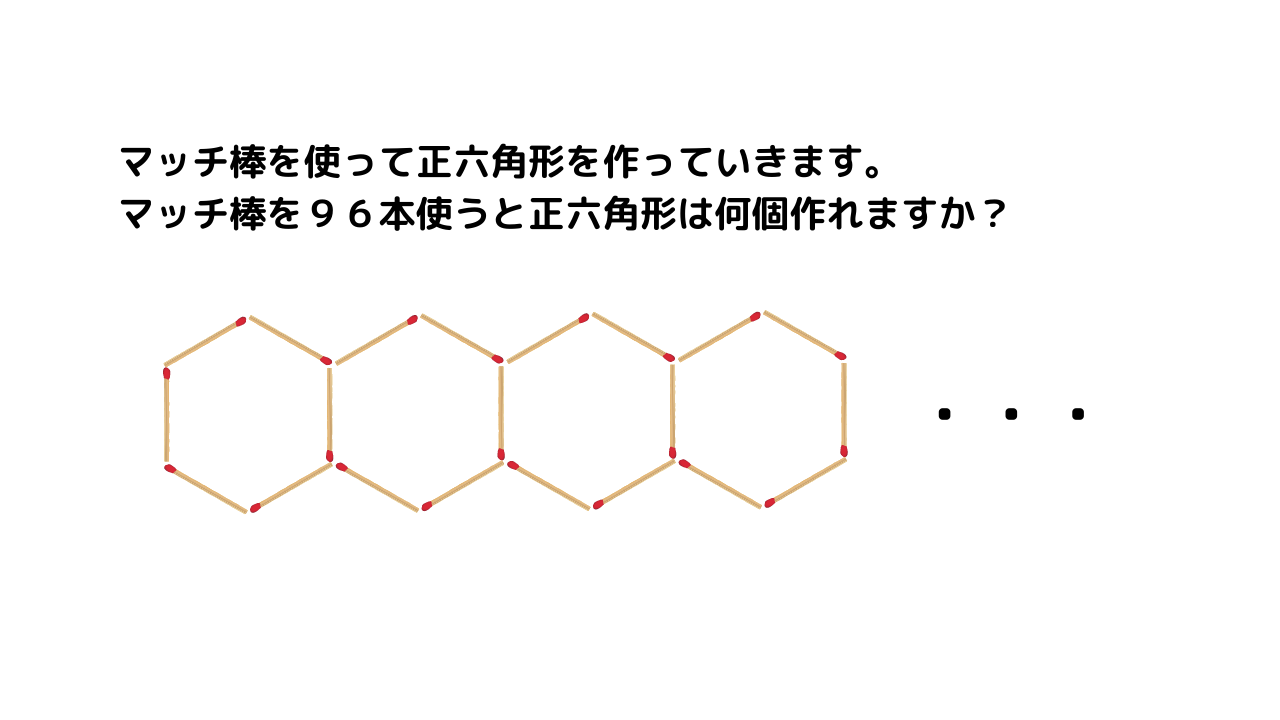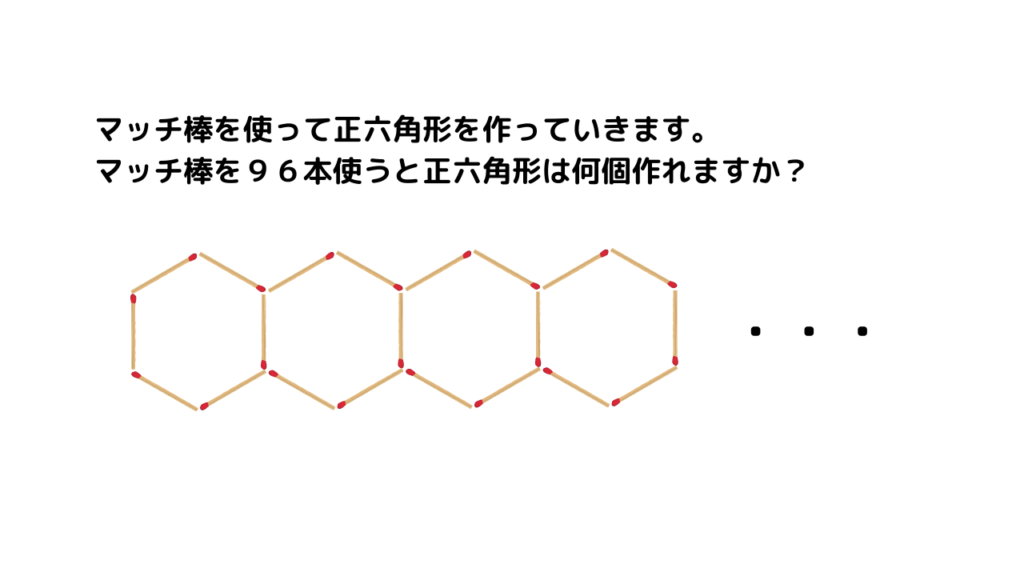
規則性を見つめる問題です。
マッチ6本で正六角形ができるのですが、上記のように隣の正六角形と共有して使えるマッチ棒があるので、それを除いた5本のマッチ棒が繰り返していくことに気づくことが鍵です。
96(本)÷5(本)=19(組)あまり1(本)
あまりの一本は最後(19組目)の正六角形の右端のマッチ棒です。それで19個の正六角形ができるというわけです。
次はこれをレベルアップした問題です。

正六角形が2段につながっていくこの問題も、共有できる部分を見つけて、それ以外の本数が繰り返されていると気づくことができたら簡単です。
243(本)÷8(本)=30あまり3(本)
あまりの3本は最後の2段につながった正六角形を完成させるために必要な本数です。
六角形は2段なので最後に2をかけましょう。
30×2=60
つまり正六角形は60個になります。
いかがでしたでしょうか?
1問目の1段正六角形は小学4年生のテキストにあった問題で、それを自分なりにアレンジしたのが2問目です。
こんなふうに算数を楽しく学べることができるような問題をつくっていきたいと思っています。
ABOUT ME